
Medtech Japan 2024
期間 : 4月17~19日
会場:東京ビッグサイト
ブース番号:長野県産業振興機構ブース内 800
私たち彩世は半導体レーザを中心とした光源モジュールなどの製品化を行っています。私たち彩世の製品は簡単なものですが、それでも
などの技術をまとめ上げたものです。ここでは私たち彩世の製品をより理解していただくため、これから彩世製品にまつわる、光学的な技術に関する解説をまとめていきたいと思います。
今では初心者向けの解説は親切な方々によってWeb 上にたくさん存在しています。ところがもう一歩踏み込もうとすると一気に大学レベルの教科書しかなくなってしまいます。それを読みこなすのは大変ですし、教科書そのものがかなり高価です。
ここでは初心者向けの解説と大学レベルの教科書との間を取り持つようなレベルの話をまとめていきたいと思います。従って、単なる比喩などによる定性的な説明は極力避けて、数式を使って具体的な説明をしていきます。
そのためには数学の基礎的な素養はどうしても必要になります。理系の大学の授業でやるような複雑な計算はやりませんが、
は必要となります。しかし例えば複素関数の定積分や、微分幾何学などは必要としないようにします。つまり数学は必要としますが、せいぜい大学の教養課程レベルにとどめるようにします。
式の変形や数値での確認など、読んでいる方自身で実行できるようにMathematica で記述したファイルを提示します。
Mathematica は便利なのですが、デスクトップ版は超高価なので、すぐ使える方は少ないと思います。しかしここにあげる予定のMathematica コードはすべてRaspbaerry Pi OS 同梱版やJupyter notebook 上で動作するWolframLanguageForJupter でも十分実行可能なものにする予定です。ぜひ試してみていただきたいと思います。
目は光を感じる器官で、人の外界に対する感覚は目からの情報に多く依存しています。真っ暗なところでは周りに何があるのかわからず、手で探ることぐらいしかできません。目で見るためには見る対象に光が当たっている必要があります。

図 1: ラ・トゥール「聖ヨセフ」
17 世紀フランスの画家ジョルジュ・ド・ラ・トゥールの有名な絵「聖ヨセフ」ではろうそくの光が大工のヨセフと彼の子の顔を照らしています。子供が父親の手元を明るくするために左手をかざしていています。異様に高く伸びたろうそくの炎からの光があたっているところは克明に描かれ、ろうそくから遠いところや影の部分は暗く沈んで何が描いてあるのかさえよくわかりません。
これはテネブローソ、あるいはキアスクーロという絵画の技法で、明暗を強調することで見る人の視線を誘って立体感をもたらし、さらに静寂や親密さ、あるい はドラマを見る人に感じさせます。ラ・トゥールはろうそくの明かりに照らされた人物の絵をたくさん描いています。17 世紀には現在の電燈のような灯りはなく、屋内は昼間でも薄暗いのはあたりまえで、夜になれば部屋のすみなどは真っ暗になるのが普通でした。

図 2: 「聖ヨセフ」の足元の部分
絵画では光の強弱を表現の手段として使います。写真や映画でも同様です。先ほどのラ・トゥールの絵を、図-2 のように画像加工ソフトなどで暗いところを明るくしてみてください。殺風景な部屋でふたりの人物が
ただ向き合っているだけの平板な絵になってしまいます。もとの暗い部分には本来大工 の工房にはあるはずの工具さえほとんどなく、子供は何かもわからないただの四角い箱 に座っています。父親は角材に穴を開けようとしていることはわかりますが、その角材 にはなんの目印もなく、ただあてずっぽうに開けようとしているとしか見えません。つ まり暗い部分には本来あるはずのものが何も描かれていない、ということがわかります。暗いところは人にははっきりと見えず、そのためかえって人の想像力を喚起させるよ うな作用があり、絵画、あるいは写真などでは演出のためにそれを利用しているのだ、ということがわかります。
一般的に人は明暗の強い環境では目が疲れやすく、とくに明るい部分にまぶしさを感じると見づらくなってしまいます。もういちど図-1 と図-2 を見比べてみてください。明暗を平均化した方が目が楽になるのがわかると思います(絵画としてはつまらなくなりますが)。

図 3: 望ましい照明
また、先ほどのラ・トゥールの絵では子供が左手を炎にかざしています。これは手のひらで光を反射させて、より多くの光をヨセフの手元に集める目的と、もうひとつは小さな炎からの光では影が濃くなる、つまり明るいところと暗いところの差が大きくなってしまうので、手のひらの面積ぶんだけ広がった擬似光源として作用させて、極端な明暗が起こりにくくするという目的があります。
もしもっとヨセフのためを思えば、子供は白い板か紙を手のひらの代わりにした方がいいはずです。さらに、炎のヨセフ側には薄い紙などの拡散板を配置すればもっと光は広がってヨセフの作業は楽になるはずです。つまり図-3 のようにすればいいでしょう。じっさいにこのような、風除けも兼ねた薄紙やすりガラスで作られた筒を被せるようになっている燭台もありました。

図 4: レフ板(Wikipedia から)
ヒトの視覚は視細胞の感度と瞳孔の大きさを調整して、光の量が多くても少なくてもある程度の対応ができるようになっています。しかし網膜のある部分にある特定の視細胞の感度を調整することはできません。つまり視野の中に明るいところと暗いところが同時にある場合にはその調整機構は役には立ちません。
先ほども書いたように、視野の中で強い明暗がある情景は目が疲れやすく、暗いところにあるものは見えなくなるので、絵画的な演出が目的でないなら、できるだけまんべんなく一様に光が届いていることが望ましいということになります。
均一照明のために現在ではいろいろな手段が考案されています。例えば図-4 のレフ板などを見かけることもあると思います。これは反射光を拡散させる作用があります。透過型のものはたとえば 1 眼レフのホットシューに取り付けるストロボの発光源の窓についています。
拡散板は図-5 にあるように基本的には入ってきた光をいろいろな方向に広げる機能があります。
入射光束の強度分布がどんな形になっていたとしても、拡散板を透過したあと、拡散板の正面では強度分布が均一化されていきます。
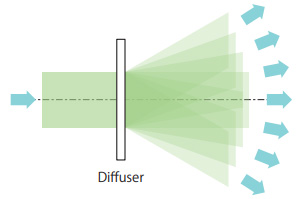
図 5: 拡散板の働き
拡散板の機能による均一化を確かめるために数値実験をしてみます。
ある幅の窓に強度が場所ごとに正規分布にバラついた光が入ってくるとします。これは極端な例で、ある場所とそのすぐ隣との光強度が無相関というのはありえないのですが、わかりやすくそうしておきます。
拡散板を透過すると図-6 のように強度分布がずらされていきながら重なることになります。
これがいくつも重なるとどうなるかを計算したのが図-7 です。
図中左のちいさな箱にあるのはそれぞれ数字の回数だけ横ずらしして足したもの、右の図はそれを同時に描いたものです。台形形状になるため上辺の長さは減っていきますが、その代わりギザギザしたノイズは減っていって平たくなっていくのがわかります。

図 7: 数値実験の結果
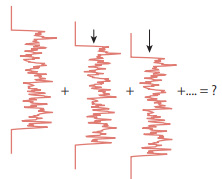
図 6: 拡散板の効果の数値実験
一般に N 個の場所にそれぞれ強度が正規分布をしたノイズがあって、そのノイズの大きさの目安をRMS
\begin{equation} \mathrm{RMS}=\sqrt{\frac{1}{N} \sum_{i}^{N}\left(x_{i}-\bar{x}\right)^{2}} \end{equation}で表すとします。ここで x¯ は xi の平均値です。これを横ずらしして M 個重ね合わせたときのノイズの大きさRMSM は
\begin{equation} \mathrm{RMS}_{M} \approx \frac{1}{\sqrt{M}} \end{equation}なることが言えます。つまりたくさん重ねるほどノイズは小さくなっていきます(この話が目的ではないので証明は省略します)。

図 8: 光強度分布を均一化する素子の例
このように拡散板には強度分布を均一化する機能があります。以前はただのすりガラスで、パラメータといえば粗度だけだったものが、最近では微細加工の技術によって拡散方向の制御など、いろいろなパラメータが指定できるようになっています。
また、図-8 のようなライトパイプやフライアイレンズといった素子もあります。これらは拡散板とは違った用途に利用されますが、基本的な原理は上に示した拡散板と同じで、光の強度分布の均一化のための素子です
白熱電灯や LED などの光は拡散板やその他の光学素子で光の強 度分布を均一化することができます。一方、レーザ光のようにコヒーレントな光は、白熱電球やLED の光と違って拡散板を通すとスペックル(Speckle)というノイズが出てしまいます
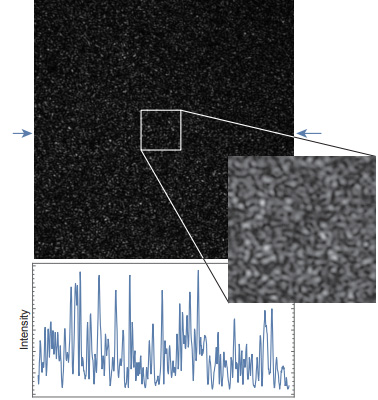
図 9: スペックルの例
図-9 は半導体レーザの光を拡散板に反射させたときの光強度の分布を示したものです。下のグラフは矢印の直線の上の強度分布です。このように細かな粒状のノイズが現れます(これはまた別のところでお話しします)。光が拡散板のような粗面で反射すると、図-10 のように光路長の異なる光が同じ位置に到達するので、普通の光では均一になるはずですが、レーザではコヒーレンシが高いため干渉が起こって光の強弱が発生します。
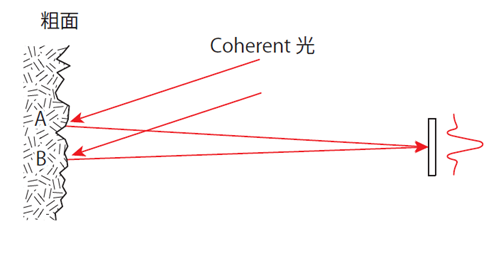
図 10: スペックルの発生
これではとても「均一な照明」とは言えません。
つまり、白熱電灯や LED では光の強度分布を重ね合わせることで均一化できたのですが、レーザの光に同じことをするとかえってノイズが増えてしまって、重ね合わせるという手法が使えない、ということになります。
しかしスペックルは干渉の結果なので、干渉が起こらなければスペックルは発生しません。干渉が起こらないようにするには、異なる光路長の光が同じ点に到達しなければいい、ということになります。その上で強度分布が均一になるようにするにはひと工夫が必要です。
図-11 にあるレンズをみてください。
これは左から平行光入射して、右へ平行光射出する、いわゆるアフォーカル(Afocal) レンズという、焦点距離無限大のレンズです。図中、細い黒線は光線追跡という計算法(その内容はいずれここで話をしたいと思います)で計算した光線の透過の仕方を表しています。それぞれの光線は交わることがなく、したがってレーザ光束の中にこのレンズを入れたとしても(入れる前にスペックルがないなら、入れたことによって)スペックルの発生はないということがわかります。
また、左側に縦を向いた矢印が描いてありますが、これは光線 4 本分の幅を表しています。レンズに入る前左側では矢印の長さはみな同じですが、レンズを透過したあとは矢印の長さが違っていて中央は長く、端に行くほど短くなっています。つまり、光線の密度が入射前後で変わるようなレンズになっています。
極端な例えですが、光線 1 本がフォトン(光の粒子)1 個に対応しているとしましょう。光の強度はフォトンの数に比例します。単位面積あたりの光の強度はそこにフォトンが何個到達したか、に比例します。光線密度が変わるということは、単位面積あたりの光強度が変わる、ということです。
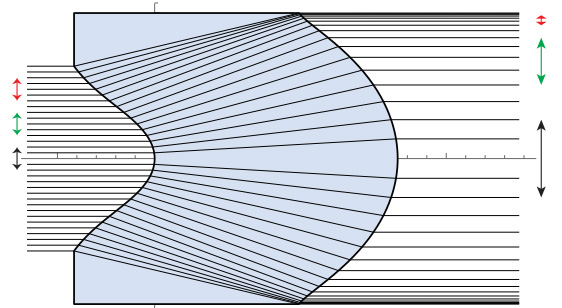
図 11: アフォーカルレンズ
図-11 のレンズの機能を説明する前に、少し寄り道をします。
光源の特性としていろいろなものがあります。分光強度(分光光度)とエネルギー効率はかならず問われます。それ以外に重要な特性として発光面積(とその形状)と角度分布があります。例えば電球ではフィラメントが発光体なので形状は複雑ですが、フィラメントそのものからはどの方向にも 360 °(厳密に言えば 4πsr(ステラジアン))同じ強度で光が出ていきます。
LED ではたいてい四角い平面の発光体で、その前面から光が出ますが、裏からは出ません。また、面の垂直方向には光は多く、面スレスレに出てくる光は少なくなっています。これらは発光原理によっておおよそ決まっています。
一方レーザはその発光媒質の大きさに比べるとずっと小さな発光面積になっています。少なくとも出てくる光は小さな一点から出てくるように見えます。また角度分布はLED などに比べるとずっと狭く、ほとんど広がらずに出てきます。
この発光体がほぼ点に見えることと、ほとんど広がらないことから、レーザ光を目で直接覗き込むと、水晶体によって発光点が網膜に結像して、そこにレーザから出てくる光のほぼ全てが集中するため、網膜を焼いてしまう可能性があります。他の光源ではよほど強いものでない限り網膜を焼く心配はないため、レーザにだけ安全基準が設けられています。
またレーザは特定の角度分布を持っているものが多くなっています。それは発光効率を高めるための一つの条件になっているため、レーザの設計上そうある必要があるからです。
ある角度θrad 方向に出る光の強度を I(θ) とすると
\begin{equation} I(\theta) \propto e^{-2\left(\frac{\theta}{a}\right)^{2}} \end{equation}というガウシアンの形になっています。ここでα は広がりの大きさを決める定数で、θ = α の方向へはθ = 0 の方向への強度の 1/e2(≈13%)になるということです。α の値はレーザごとに違っていて、例えば低パワーのHe-Ne レーザではα ≈ 0.5mrad ぐらい、半導体レーザではα ≈ 0.1 ∼ 0.5rad(≈ 8 ∼ 40 °)ぐらいです。典型的な形を図-12 に示し
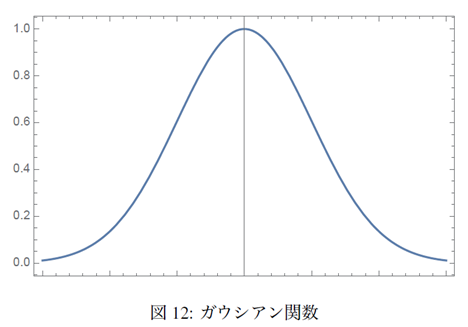
このように広がり方はレーザによっていろいろですが、ほぼすべて(特に低パワーのレーザでは)の角度分布はガウシアンの格好をしています。つまりまんなかは光が強く、外に行くほど弱くなります。
もし図-11 のレンズにガウシアンの強度分布を入射させると、均一な強度分布に変換されて出てくるのではないか、と期待できます。
このような均一な強度分布への変換をトップハット(Tophat)変換と言います。トップハットというのは男性用のフォーマルな帽子でいわゆるシルクハットのことです。この帽子のてっぺんが平らで、均一な強度分布の形がこの帽子を横から見た形と似ていて、
直感的に輪郭のイメージが湧くのでこのように呼ばれるようです。このレンズによってレーザ光をスペックルなしで均一な光の強度分布にすることができます。ただもちろんレンズによる光線密度の変化がガウシアンの形とちょうど逆になっている必要があります。また広がりのあるガウシアンではなく、平行光で入射させる必要があります。
図 13: トップハット
レンズの面形状の前に、変換素子の前後で光線がどう変われば、ガウシアンの形をトップハットにできるかを考えます。簡単のため 1 次元で、つまりある方向にだけトップハットにして、それと垂直な方向はそのまま、という場合を考えます。
とりあえず変換素子の面がどんな形になるかは別にして、光線がどう変換されればいいかを考えます。また、回折は考慮せずに幾何光学的に考え、さらに光軸に対して対称だとします。
また平行光入射を仮定しているので、どうやって平行光にするかはとりあえず置いておいて、入射側強度分布を中心(光軸)からの距離(光軸高さ)で表します。つまり入射側での光軸からの距離を h としてその位置での強度を Ii(h) と表します。つまり
\begin{equation} I_{i}(h)=e^{-2\left(\frac{h}{n_{0}}\right)^{2}} \end{equation}とします。ここで h0 は強度が光軸上の 1/e2 になる高さです。
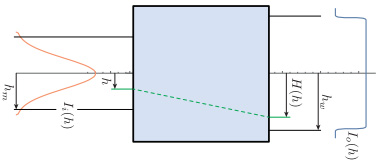
図 14: 光線密度の変換
ガウシアンは高く(h が大きく)なるほど強度は急速に低くなりますが、0 にはなりません。そこである高さ hm までをトップハットに変換して、その外は捨てるということにします。そしてトップハットの端の高さを hw とします。したがって、hm の光線は出るときには hw になっている、ということになります。
図-14 のように、入射側の高さ h の光線が射出側で高さ H(h) になるとします。当然
\begin{equation} \begin{array}{r} H(0)=0 \\ H\left(h_{m}\right)=h_{w} \end{array} \end{equation}です。そして射出側の高さ h での強度を Io(h) とします。
入射側の高さ h での高さ方向の微小長さ dh は射出側では
\begin{equation} d h^{\prime}=\frac{d H(h)}{d h} d h \end{equation}となり、変換素子内部でのロスがないとすると dh に入る光強度はすべて射出側に出るので
\begin{equation} \begin{aligned} I_{i}(h) d h &=I_{o}(H(h)) d h^{\prime} \\ &=I_{o}(H(h)) \frac{d H(h)}{d h} d h \end{aligned} \end{equation}のように入射側と射出側で一致するはずです。
また全光量も一致するはずとして
\begin{equation} \begin{aligned} \int_{0}^{\sqrt{l_{m}}} d h I_{i}(h) &=\int_{0}^{\sqrt{l_{m}}} d h I_{o}(H(h)) \frac{d H(h)}{d h} \\ &=\int_{0}^{h_{w}} d h I_{o}(h) \end{aligned} \end{equation}となります。
ここで、入射側の強度分布はガウシアンで、射出側はトップハットにしたいので高さによらず定数
\begin{equation} I_{o}(h)=\Upsilon_{0} \end{equation}とします。式-7 は
\begin{equation} \begin{aligned} \int_{0}^{h_{m}} d h e^{-2\left(h / h_{0}\right)^{2}} &=\int_{0}^{h_{w}} d h^{2}_{0} \\ &=\Upsilon_{0} h_{w} \end{aligned} \end{equation}なので
\begin{equation} \Upsilon_{0}=\frac{h_{0}}{h_{w}} \sqrt{\frac{\pi}{8}} \operatorname{erf}\left(\sqrt{2} \frac{h_{m}}{h_{0}}\right) \end{equation}となります。ここでerf(z) は誤差関数と呼ばれて
\begin{equation} \operatorname{erf}(z) \equiv \frac{2}{\sqrt{\pi}} \int_{0}^{z} d t e^{-t^{2}} \end{equation}です。この積分は初等関数では表せないので、積分の形のままで定義されています。式-6 は
\begin{equation} \begin{aligned} e^{-2\left(h / h_{0}\right)^{2}} d h &=\Upsilon_{0} \frac{d H(h)}{d h} d h \\ \frac{d H(h)}{d h} &=\frac{e^{-2\left(h / h_{0}\right)^{2}}}{\Upsilon_{0}} \end{aligned} \end{equation}なので、H(h) の形が決まって
\begin{equation} \begin{aligned} H(h) &=\frac{h_{0}}{\Upsilon_{0}} \sqrt{\frac{\pi}{8}} \operatorname{erf}\left(\sqrt{2} \frac{h}{h_{0}}\right) \\ &=h_{w} \frac{\operatorname{erf}\left(\sqrt{2} \frac{h}{h_{0}}\right)}{\operatorname{erf}\left(\sqrt{2} \frac{h_{m}}{h_{0}}\right)} \end{aligned} \end{equation}となります。
誤差関数がピンと来ませんが、図-15 のような形になります。
例として、h0 = 1、hm = 1、hw = 1.5 の場合の光線の様子をプロットしたのが図-16 です。

図 15: 誤差関数
そしてこうなるためには面はどんな形状でなけらばならないかを計算したのが図-11 でした。2 面でこの光線を実現するためには両面が非球面でなければなりません。面形状の決定は汎用のレンズ設計ソフト(Zemax やCodeV)などによる最適化計算で可能です。また、ある条件では最適化によらず数値積分を行うことによっても決定できます。しかし、それは非常に大きな式を扱うことになるので、ここではやりません。

図 16: 計算結果の例
前節ではアフォーカルな例を示しました。しかしこれではレンズの径よりも広い範囲を照明することはできません。レンズは小さく、照明範囲は広くするほうが望ましいと考えられます。
そのためにはどうすればいいか、というのはすぐ思いつきます。つまり図-17 のように光線を扇型にして照明範囲を広げればいいのです。
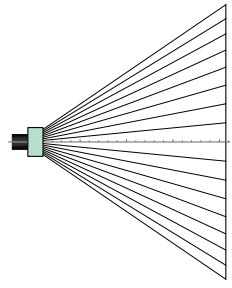
図 17: 照明範囲拡大
ここで一点気をつけなければいけないことがあります。アフォーカルなレンズでは照明対象の平面に光線はすべて垂直に入っていました。ところがこの図のような光学系によると、光線の入射する角度が場所によって違ってきます。そのような場合の光強度というのはどう考えればいいのでしょうか?
図-18 のように、幅 d の窓に光束が広がりながら入射する場合を考えます。そして平行光束が窓の法線に対してθ だけ傾いて入ってくるとします。
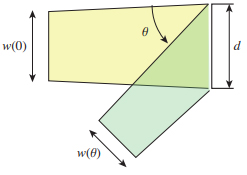
図 18: 窓に入射する光束
窓を通過できる光束の幅を w(θ) とすると
\begin{equation} w(\theta)=d \cos \theta \end{equation}となることは幾何学的な計算からすぐわかります。つまり、窓に対して斜めの光束は窓を通過する光量が減ってしまう、ということです。逆に言えば同じ太さの光束でも斜めにしてやれば広い範囲を照明できるということで、その分単位面積あたりの光量は減る、ということです。
照明技術の言葉で言えば、物体表面の単位面積あたりに入射する光束の量を照度、il-luminance と言います。同じ強度の光束でも照明したい表面に斜めに入ると光束の量が減り、つまりはその分暗くなるのを考慮した量です。
照度の定義は厳密には、物理量ではなく目の波長あたりの感度で補正された量ですが、単一波長で絶対値を問わない場合は気にする必要はありません(なぜか照度に対応する物理量、例えば次元がW/m2 となるような量に名前はついていません)。
図-17 のような光学系で「均一な照明」とするためには、この斜め入射の効果を考慮する必要があり、均一性の評価は「光の強度」ではなく「照度」でする必要があります。
さらに、平行光ではなく広がりながら進む光束では光源からの距離も影響することは直感的にわかります。
前節のアフォーカルな例では平面に対して照射した場合、どの光線も同じ角度で面に入射するので「光強度」と「照度」が曖昧でも問題ありませんでしたが、図-17 ではそれぞれの光線の面に入射する角度を考慮する必要があります。この場合の「照度」を均一にする変換を考えてみましょう。

図 19: 広がる光束で均一な照明
アフォーカルな場合にしたがって、図-19(A) のように素子の光軸から高さ h で光軸に並行に光線が入射して素子を透過後、角度θ で出ていって素子から距離 D だけ離れた、光軸に垂直な平面を 1 次元的に照明する(紙面に垂直な方向には素子は何も作用しない) とします。また、簡単のため、
\begin{equation} h \ll D, H \end{equation}とします。つまり素子から照明面までは十分遠く、H h H とみなせるということで、照明面積に比べて素子の大きさは無視する、ということです。つまり図-19(B) のように
\begin{equation} H=D \tan \theta \end{equation}とみなします。この前提で θ(h) がどういう形になれば照明面で均一になるかを考えます。
入射側での微小高さ dh が照明面での dH にどう対応するかを考えると
\begin{equation} \begin{aligned} d h &=\frac{d h}{d \theta} d \theta \\ &=\frac{d h}{d \theta} \frac{d \theta}{d H} d H \end{aligned} \end{equation}なので、式-14 から(0 ≤ θ < π/2 として)
\begin{equation} d h=\frac{d h}{d \theta} \frac{\cos ^{2} \theta}{D} d H \end{equation}となります。cos2 のうちひとつは前節で説明した斜めに入ることによる係数と、もうひとつは dH までも距離が D/ cos θ で遠くなるためにかかる係数だと解釈できます(これが 1 次元の話であることをお忘れなく)。
dh に入る光量は Ii(h)dh なので
\begin{equation} I_{i}(h) d h=I_{i}(h) \frac{d h}{d \theta} \frac{\cos ^{2} \theta}{D} d H \end{equation}照明面で Io(H)dH を一定にしたいので dH にかかった部分が定数Υ0 であるとして
\begin{equation} \Upsilon_{0}=I_{i}(h) \frac{d h}{d \theta} \frac{\cos ^{2} \theta}{D} \end{equation}θ(h) は一価関数なので
\begin{equation} \frac{d \theta}{d h}=1 / \frac{d h}{d \theta} \end{equation}としてよくて、式-15 は
\begin{equation} \frac{d \theta}{d h}=\frac{I_{i}(h) \cos ^{2} \theta}{\Upsilon_{0} D} \end{equation}となります。これをθ(h) に関する微分方程式とみなして、Ii(h) を式-4 とおいたうえで解けばいいのですが、結構難物です。計算はソフトウェアに任せると
\begin{equation} \theta(h)=\tan ^{-1} \frac{h_{0} \sqrt{\pi / 2} \operatorname{erf}\left(\sqrt{2} \frac{h}{h_{0}}\right)}{2 D^{\Upsilon}_{0}} \end{equation}となります。Υ0 はアフォーカルな場合と同じように、高さ hm までの光線を角度θw の光線に変換するとしてそこまでの光量を積分することで決めることができます。これも比較的大きな式になりますのでここでは計算しません。
アフォーカルの場合と同じようにα = 1、hm = 1、θw = 45 °の場合の光線を図-20 に示します。
以上の原理によって私たちの製品Lineman は設計され、そして評価されています。他社の製品では以上で説明した光強度と照度の区別があいまいなまま仕様化されているものも見受けられますが、私たちのLineman は以上のように厳密に定義され、それにしたがって設計/評価されていることをここで強調させていただきます。ここでは私たちの製品にまつわる原理や光学の問題のトピックを順次取り上げていきたいと思います。
ご期待ください。
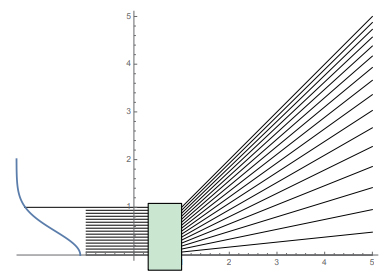
図 20
高い光線はほとんど 45 °方向に出て光線密度が上がっていることがわかります。これも実際の光学素子で実現するには非球面が必要となります。