彩世の光学技術者が論文をOptikに投稿しました。現在オンラインで公開されていて誰でもタダで読むことができます。

論文の内容は

• 単玉非球面レンズ2面の形状を数値積分で決定
• 球面収差とコマ収差が「完全に」補正されたレンズの面形状が瞬時で得られる
• 近軸量を初期データとして与えるだけ
• 同様の設計手法でトップハット変換レンズや、ベッセルビーム生成レンズなどが設計可能であることを証明
• Mathematicaで実行可能な設計ソフトを公開、ソフトはRaspberry Pi同梱のMathematicaでも実行可能

 

というものです。

これまでカメラ用ズームレンズや顕微鏡対物レンズ、レーザ用のコリメータまで全てのレンズ設計はいわゆる「最適化」の手法で行われていました。これはコンピュータの上でレンズの光学的な特性をシミュレートして、必要な性能に達するまでカットアンドトライを繰り返すもので、どんな設計にも対応できますが、

• 過程によって結果が異なる
• 解があるかどうかやってみないとわからない
• いつ終わるかわからない
• 最終結果に「良い悪い」がつきまとう
• 設計者の経験と勘が必要

 

などの問題がありました。

 

今回の論文では

• 非球面を2面持つ
• 他に面が複数あってもよいが、固定されているものとする
• 回転対称である
• 光軸上から出る光線束のみ扱う

 

という制限の上で

• 近軸パラメータ（光軸付近のレンズパラメータ）を与える
• 数値積分によりふたつの非球面の形状を決定する

 

を行ってレンズ設計ができることを示しました。

 

論文のもとになっているのは70年以上前の1949年に出版されたWassermannとWolfによる「On the theory of aplanatic aspheric systems」という論文に出てくる方程式です。それはこんな格好をしています。

 

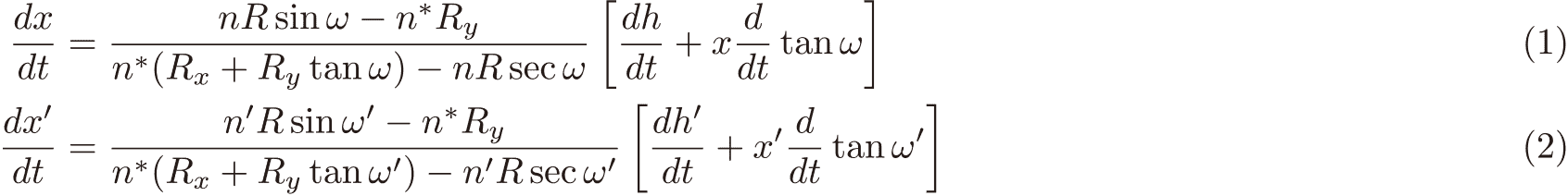
これは2変数の非線形斉次常微分方程式で、x(t)とx'(t)が面の形状を表します。これを数値積分することで非球面形状を決定します。

 

この方法によると

• パラメータを決めると面が一意に決まる
• 面形状決定に要する時間がほぼ一定
• 与えたパラメータに対する解があるかどうかはそのパラメータだけで決まる
• 数値積分ができれば誰でもでき、誰でも同じ最良解に到達する
• パラメータが従来方法に比べて少ないので、パラメータ間の最適化も容易

という特徴があります。

 

ただし、上に述べた制限があるため、どんなレンズにもこの手法が使えるわけではありません。例えば撮像用のレンズなどで、いろいろな画角での特性をまんべんなく良くしたい、というような設計はできません。しかし、レーザコリメータや光ディスク用の対物レンズの設計にはこれまでのCodeVやZemaxなどの最適化ソフトウェアは、これでまったく必要なくなったと言えます。

また、論文内で示したように、トップハット変換レンズやベッセルビーム生成レンズなど「結像しないレンズ」も設計可能となります。これ以外にもいろいろな応用が考えられます。

デモンストレーションのために実際に設計に利用できるコードをGitHubで公開しています。

このコードはすべてMathematicaで書かれています。Mathematicaは非常に高価なソフトウェアで誰でもが使えるわけではありませんが、関数をひとつ呼ぶだけでこの数値積分ができてしまうので非常に便利です。
実はその高価なMathemeticaが現在Raspberry Pi OSに同梱されていて、誰でもタダで使うことができます（たいていのRaspberry Piユーザは新しくOSをインストールするとまずMathematicaを消してSDカードの空き領域を増やすのが当たり前になっていますが、それはもったいない話です）。そしてこのデモンストレーションコードはRaspberry Pi OS版でも実行が可能です。

実際にRaspberry Pi 4 Model B上のRaspberry Pi OSで動作させている動画をYouTubeに投稿しました。

高いハードウェアパフォーマンスが必要ではなく、Raspberry Piの全てのモデルで実行可能です。もちろんパフォーマンスの高いほうが望ましいですが、最もパフォーマンスの高いRaspberry Pi 4 Model Bでも1万円以下で手に入るのでちょっと試してみる、ということも簡単です。光学あるいはレンズ設計が専門ではない方でも簡単に非球面レンズ設計をすることができます。
例えば専門家でも設計に苦労するBlu-ray用対物レンズを設計してみましょう。N.A.（Numerical Aperture）は0.9、使用波長は405nm、焦点距離=3mm、硝材（レンズ本体の材料）をSF-10（405nmでの屈折率が1.7756）、ディスク厚0.1mmとして、適当な近軸量を与えてやると

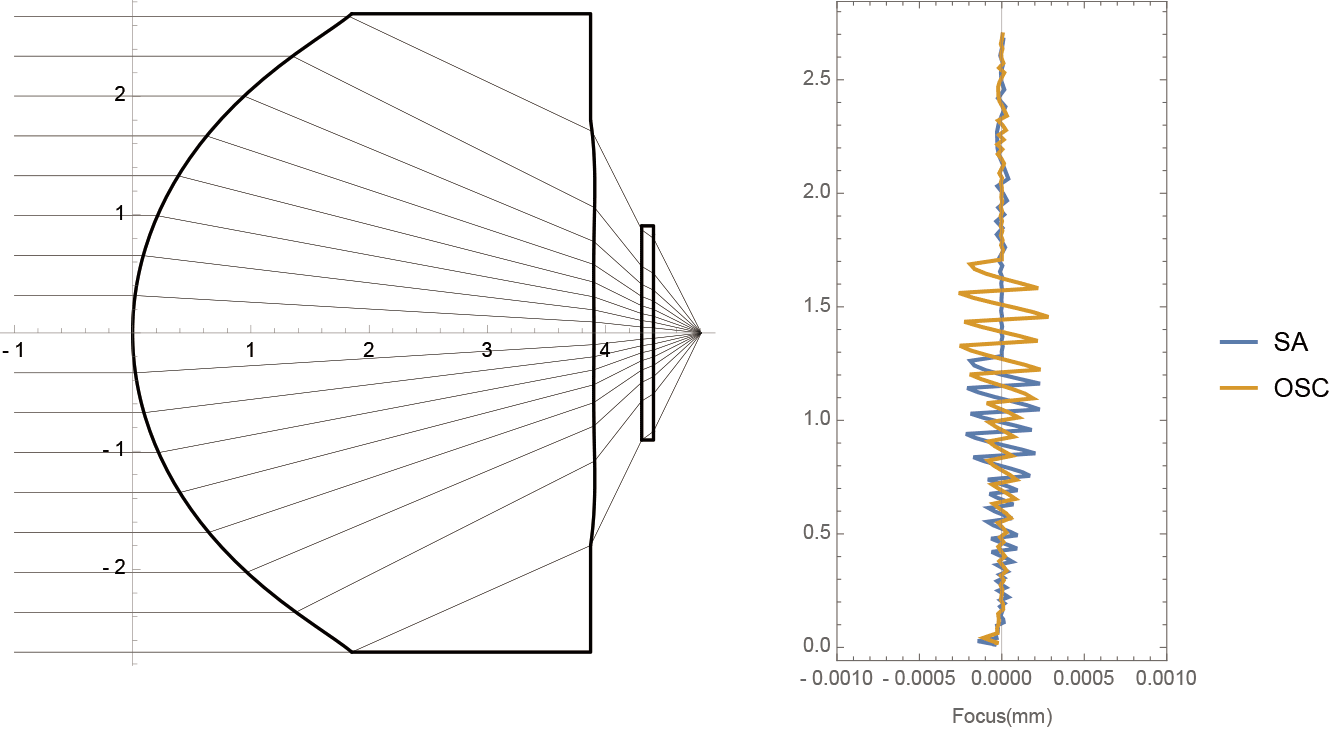
というようなものが1秒以下でできます（図の右側はいわゆる縦収差図で、レンズの性能を表しています。SAは球面収差、OSCは正弦条件違反量です。縦軸は入射光線の高さ、横軸は光線が光軸と交わる位置で、図の幅はｱ1μmです）。

もちろん、与える近軸量によってはN.A.が0.9に到達せず、それよりも低いN.A.の解しか得られないことがあります。しかしそれは設計者の技術が足りないのではなく、与えられたパラメータでは解が物理的に存在しないからなのです。
このコードはMathematicaのメーカであるWolfram ResearchのコミュニティサイトでStuff Pickにも取り上げられました。

興味のある方はぜひ試してみてください。