半導体レーザの信頼性（バスタブ曲線、ワイブル分布、スクリーニング）

半導体レーザ製品の寿命や信頼性は使用者にとって重要な特性です。半導体レーザを使用した製品の不具合がレーザの不点灯であったという話はしばしば聞かれます。しかし半導体レーザメーカー問い合わせたところ MTTF 等の用語が出てきて、何のことやら良く分からないという話も聞きます。半導体レーザ製品の寿命はワイブルプロット、MTTF 及びスクリーニング等の技術用語表されることが多く、慣れていないと直感的に理解しにくいところがあります。本稿ではこれらの寿命や信頼性に関わる用語のバックグランドや意味を解説します。

半導体レーザに限りませんが、製品を使用するときの故障率の時間推移は次図のようになります。その形状からバスタブ曲線と言われています。

図 1 バスタブ曲線

製品の故障率は時間に対して一定ではなく以下の 3 つの領域に分類されます。

初期故障領域 ：導入当初は部品の不良や調整の不良による故障が発生しますが、取替や修正により、時間とともに故障確率は減少します。

偶発故障領域 ：初期故障がほとんどなくなると安定状態になります。しかし、偶発的な故障は発生しますので、故障率は一定の値になります。

摩耗故障領域 ：長期間使用していると、部品の劣化が起こり、時間とともに故障が多くなります

このような一連の故障率の推移は、半導体レーザに限らず多種多様な分野で見られます。どの分野においても製品として好ましいのは生産が安定し初期不良が取り除かれた状態、つまり偶発故障期間のものの使用になります。

半導体レーザメーカーは、自社のレーザの初期不良が十分に取り除かれた状態であることを確認する必要があります。この確認作業で使用されるのがワイブル分布です。ワイブル分布は、上述の３つの故障確率を数式化するのに適した確率分布です。この分布を用いることよりバスタブ曲線を数学的に記述でき様々な分析や判定を行うことができます。ワイブル分布は、数式で次のように表現されます

確率密度関数：時刻 t まで故障せず時刻t で故障する確率

\begin{equation} f(t)=\frac{m t^{m-1}}{\eta^{m}} \cdot e^{-\left(\frac{t}{η}\right)^{m}} \end{equation}

故障率：時刻 t で故障する確率

\begin{equation} \lambda(\mathrm{t})=\frac{m t^{m-1}}{\eta^{m}} \end{equation}

信頼度関数：時刻ｔまで故障しない確率

\begin{equation} R(t)=e^{-\left(\frac{t}{η}\right)^{m}} \end{equation}

累積故障率：時刻ｔまでに故障する確率

\begin{equation} F(t)=1-R(t)=1-e^{-\left(\frac{t}{η}\right)^{m}} \end{equation}

m：形状パラメータです。分布の形を代表する係数でワイブル係数と言われます。

η：尺度パラメータです。時間のスケールを規定する係数です。

実際には半導体レーザメーカーは自社での寿命試験、一般にエージング試験と言いますが、このエージング試験結果を累積故障率Ｆ(ｔ)としてワイブル確立紙にプロットします。エージング試験は一般には最大動作保証温度で千時間オーダー行い、エージングカーブを外挿 して各々の故障時間推定します。累積故障率Ｆ(ｔ)をワイブル確立紙にプロットするとこれから形状パラメータや時間パラメータが推定できます。推定された両パラメータから半導 体レーザの信頼性に関する情報を得ることが出来ます。具体的には下記の手順を参照して ください。

図 2 エージングカーブ

図 2 はN=30、2000h のエージングカーブ例です。縦軸は半導体レーザの動作電流の増加率です。一般にある一定の増加率に達すると故障とする例が多く、ここでは増加率 20%を故障と定義しています。5 個故障しており、1000,2000,3000,4000,5000h で 5 個が故障しています。（3000,4000,5000h はカーブを外挿しています）。この結果をワイブル確立紙にプロットしますと下図になります。

図 3 ワイブル確率紙

次に形状パラメータと尺度パラメータについて説明します。

形状パラメータ：

ワイブル確率紙の右軸は上式より

\begin{equation} \ln \ln \{1 /[1-F(t)]\}=\operatorname{m} \ln (t)-\operatorname{mln}(\eta) \end{equation}

と表されます。またワイブル確率紙の上軸は ln(𝑡) です。

\begin{equation} X=\ln (t), \quad Y=\ln \ln \{1 /[1-F(t)]\}, \quad b=\operatorname{mln}(\eta) \end{equation}

としますと Y=mX+b になります。

したがってプロットしたＦ(ｔ)の傾きからから形状パラメータ m 値を推定することができます。具体的には以下の手順です。

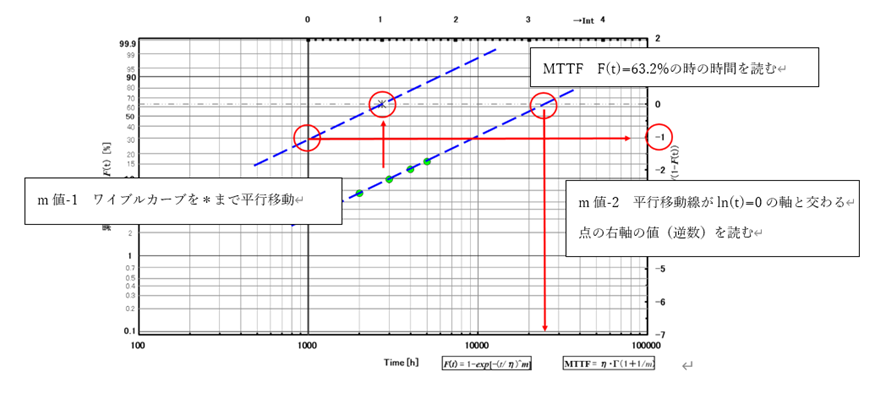
図4 ワイブル確率紙の使い方

m=１：時刻ｔに関係なく故障率λ(t)は一定になります。m=１はこの製品が偶発故障領域に属すると見ることができます。m＝１のときワイブル分布は指数関数になります。ワイブル分布は元々指数関数を拡張した関数だからです。

\begin{equation} R(t)=e^{-\left(\frac{t}{\mathrm{η}}\right)} \end{equation} \begin{equation} \mathrm{F}(\mathrm{t})=1-\mathrm{R}(\mathrm{t})=1-e^{-\left(\frac{t}{\mathrm{η}}\right)} \end{equation}

０＜m＜１：故障率λ(t)は次第に緩やかになる右下がりの曲線になります。初期故障領域と見ることができます。

１＜m：故障率λ(t)は次第に急になる右上がりの曲線で m 値が大になると急激に増大します。摩耗故障領域と見ることができます。

尺度パラメータ：

m=1 の指数関数の場合、1/ηは MTTF(Mean Time To Failure)と呼ばれ指数関数を表す重要な時間指標となります。MTTF における累積故障率は

\begin{equation} \mathrm{F}(\mathrm{MTTF})=1-\mathrm{R}(\mathrm{MTTF})=1-e^{(-1)}=0.632 \end{equation}

となり全体の 63.2%が故障する時間を示しています。 ワイブル確立紙にプロットした縦軸63.2%を与える時間が MTTF となります。

このように半導体レーザメーカーは寿命試験を行いワイブル確立紙にプロットしたワイブルカーブを見ることで、自社の製品がバスタブ曲線のどの故障領域に位置するか、及び時間尺度の指標である MTTF の値を得ることができます。次にワイブル確立紙にプロットされたワイブルカーブの具体例を紹介します。

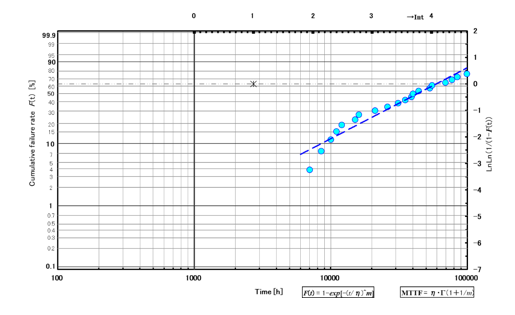
図 5 ワイブルカーブ 1

m=1.05、MTTF=60000h（N=25）です。この半導体レーザは偶発領域と考えられ、1000h付近の不良率も十分低く抑えられています。

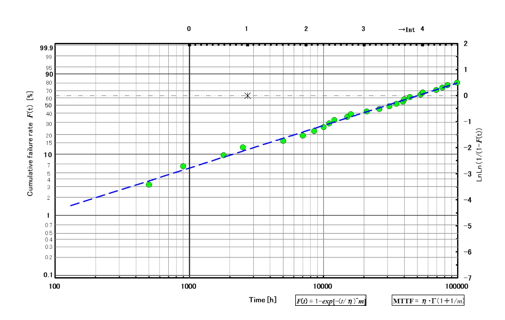
図 6 ワイブルカーブ 2

m=0.75、MTTF=50000h（N=30）です。MTTF は先例と比較して 10000h 程度の違いであるのに対し、1000h 付近の初期不良率が急減に悪化しています。この場合レーザメーカーはm=0.75 も含めて初期故障領域にあると判断し、次に述べる適切なスクリーニング手法を検討しなければなりません。

スクリーニングはレーザ製品が初期故障を含んでいる場合、これを選別し排除する手法 です。通常はレーザの静特性、例えば動作電流や閾値電流、光出力-電流カーブの微分効率などでの選別、あるいは短時間のエージングを行って初期劣化率で選別を行う等します。選別方法が明確でない場合はあらかじめ静特性値や初期劣化率付きのサンプルを長期エージ ングにかけ、ワイブルカーブを観測しながら有効な選別手段を決めていく必要があります。次図のようにスクリーニングによって初期不良 5 個をリジェクトしますと、ワイブルカーブは急速に改善する様子がわかります。

図 7 ワイブルカーブ 3

このようにワイブルカーブは半導体レーザの信頼性を確認するのに有効で広く利用されています。半導体レーザの採用を考える場合には、MTTF の値だけでなくワイブルカーブを入手し、その傾きや初期故障の有無を自社の製品信頼性仕様と照らして確認することが重要です。